Analytical micromechanics methods have much lower computational cost than Finite Element Method (FEM) or even Fast Fourier Transform (FFT)-based methods. Thus, they are widely used in both academia and industry for fast predictions of multiscale material responses.
There are several categories of analytical micromechanics methods. The first category of micromechanics methods begins from the work of Hashin and Shrikman, who gave the upper and lower bounds for the effective properties of heterogeneous materials based on variational principles. Their closed-form solutions depend on the volume fraction of the inclusion or secondary phase but ignore other key factors, such as the inclusion shapes and distributions. In order to improve the accuracy and universality of this model, higher-order bounds have been proposed which incorporate statistical microstructural information, such as two-point and three-point correlation functions.
The second category of micromechanics methods dates back to the work of Eshelby, which gave the exact solution of the stress field for one ellipsoidal inclusion embedded in an infinite matrix. Several mean-field approaches were proposed based on Eshelby’s solution, such as the Mori-Tanaka method and (generalized) self-consistent methods. Approaches based on Eshelby’s solution are usually restricted to regular inclusion shapes such as ellipses in 2-D and ellipsoids in 3-D.
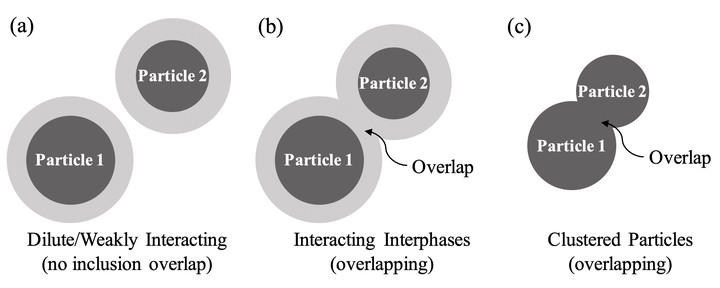
A part of my PhD thesis was on the development of an extended analytical micromechanics method that handles general overlapping inclusion geometries, which typically appear in nano-particle reinforced polymer composites. Due to particle-matrix interaction, a nano-particle is surrounded by a nontrivial interphase region with dramatically different mechanical properties. This micromechanics model has been applied to inversely determine the interphase properties, which are usually hard to be directly measured from physical experiments.